用动态因子模型估计一致指数 - EViews 14

作者兼客座作者：Eren Ocakverdi

这篇博客文章旨在介绍一个新的插件（即COINCIDENT），用于在动态因子建模框架内估计同步指数。

介绍

Stock 和 Watson（1989）提出了一种动态因子分析方法，用于构建衡量整体经济活动状况的同步指数。作者采用的模型“……基于这样一种理念：许多宏观经济变量的联动具有一个共同的元素，而这个元素可以被一个单一的潜在、未观测到的变量捕捉到。”这种单指数框架非常灵活，可以有效地用于通用的降维分析，其中目标变量被假设具有一个共同的因子。

单动态因素模型规范

让我们将表示为对数中感兴趣的变量(i=1，2，….n)和delta作为差分算子。则动态因子框架可以概括如下：

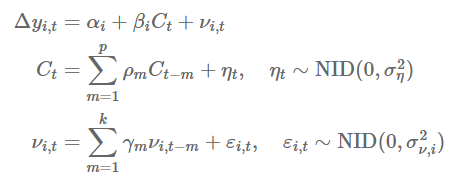
在这里，Ct 是具有 AR(p) 动态的潜在共同因子，它同时驱动我们观察到的时间序列变量（假设 p=1 且 ρm=1 将施加一个随机游走）。测量误差 ν_i,t也被定义为具有 AR(k) 动态（假设 k=1 且 γm=0 将施加白噪声）。如果每个变量都有一个共同的随机趋势成分，那么就不需要进行转换（即 y_i,t）。

适用于部门通胀预期

经济主体在通胀预期上可能存在差异，因为他们接触到的 CPI 篮子中的商品和服务种类不同。他们也可能对所偏好的商品和服务价格变化赋予不同的权重。然而，可以合理假设，可能存在一个共同成分，对每个主体对价格变化的感知或行为产生影响（COINCIDENT_DATA.WF1）。

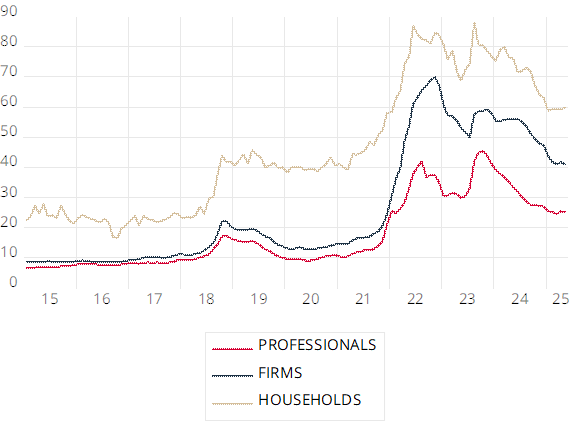
图1显示了土耳其市场专业人士、企业和家庭对未来12个月的年度通胀预期（COINCIDENT_EXAMPLE.PRG）。家庭的通胀预期最高，而市场专业人士的通胀预期最低。尽管预期水平存在较大差异，但它们之间的相关性高于0.95。

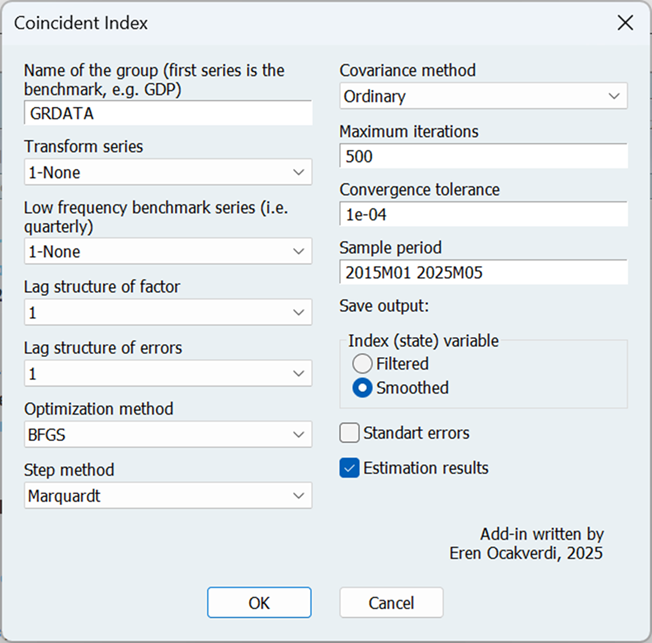
首先，我们在不对数据进行任何转换的情况下，对因子和测量误差都施加一个AR(1)滞后结构来估计模型。然后，通过使用插件，估计其他替代滞后结构以便进行比较。从方程对象调用插件将提示用户界面（见图2）。

由于我们有三个因变量，因此估计了十三个超参数（3×4+1）和四个状态变量（3+1）。估计的rho值，( \rho_1 )，接近1表明潜在因子可能具有随机趋势，而gamma值，( \gamma_m )，高于0.9也表明围绕潜在因子的持续性行为（见表1）。

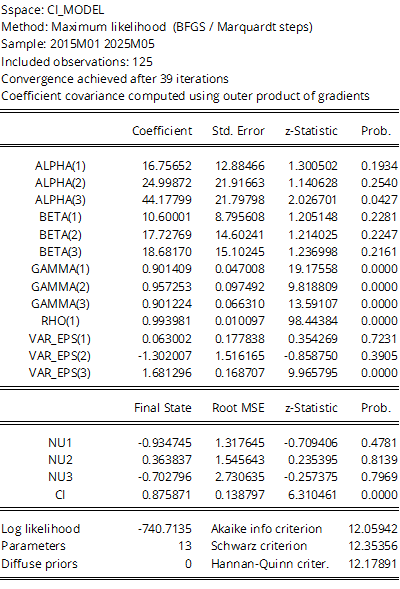
潜在因子变化1个百分点对家庭预期的影响约为19个百分点，略高于对企业预期的影响（即 ( \beta_2 ) 和 ( \beta_3 )）。然而，市场专业人士似乎对这种变化相对不那么敏感（即 ( \beta_1 )）。预期水平的差异由尺度参数（即alpha，( \alpha_i )）捕捉。需要注意的是，不同的滞后结构可能会导致不同的结果（见图3）。

图3：不同滞后规范的同步指数比较

我们可以使用一个参考（低频）序列作为提取共同因子的基准。在这种情况下，我们需要一个额外的测量方程来关联参考序列与未观测的指数变量：

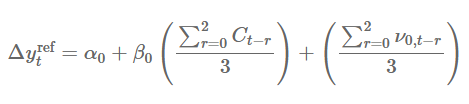
在这里，参考序列 ( \Delta y_{\text{ref},t} ) 是 GDP 平减指数的年变化率，用以反映总体价格动态，并且每三个月观测一次。

在疫情之前，各部门预期的平均值系统性地高于实际数据，而估计的指数在拟合方面表现更好。此后，非常高的通胀实现值导致这两个指标都出现了显著的跳跃，但在通胀开始下降之前，指数在捕捉水平变化方面仍然优于各部门预期的平均值（见图4）。

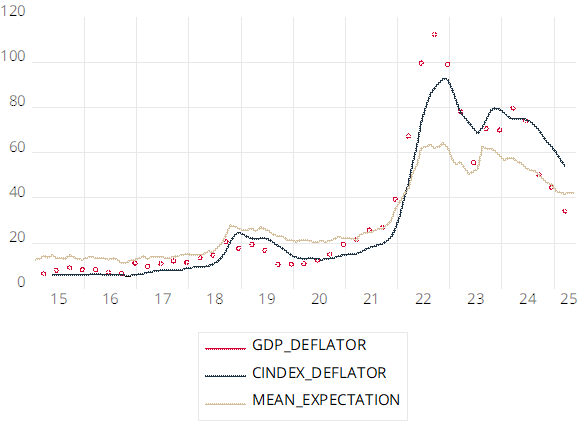
除了用于即期预测或估计经济状况外，单指数框架在降维问题中也非常有用，你需要对现有的信息进行总结，并将其提炼为一个单一指标。

文件

参考

Stock, J. H., and Watson, M. W., (1989), “New Indexes of Coincident and Leading Economic Indicators”, NBER Macroeconomics Annual, pp. 351-94.

目录

介绍

单动态因素模型规范

适用于部门通胀预期

文件

参考